Orthogonale Projektion Beispiel | Dazu betrachten wir die linear unabhängigen vektoren. Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also Orthogonale projektion · orthogonalprojektion · senkrechte projektion. In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren.
Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Orthogonale projektion · orthogonalprojektion · senkrechte projektion. Dazu betrachten wir die linear unabhängigen vektoren. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren.

Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern. Dazu betrachten wir die linear unabhängigen vektoren. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren. In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also Orthogonale projektion · orthogonalprojektion · senkrechte projektion.
Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren. Dazu betrachten wir die linear unabhängigen vektoren. In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz.

Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren. Dazu betrachten wir die linear unabhängigen vektoren. In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also Orthogonale projektion · orthogonalprojektion · senkrechte projektion. Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern.
Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern. Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Orthogonale projektion · orthogonalprojektion · senkrechte projektion. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren.
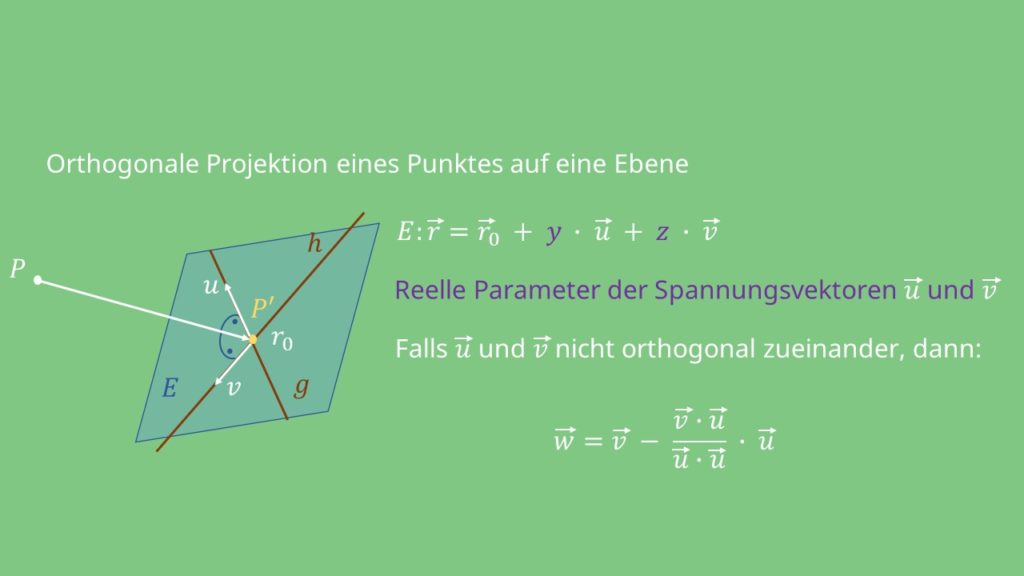
Dazu betrachten wir die linear unabhängigen vektoren. Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren. In der syntax zum beispiel wird mit diesem begriff die rolle, die wortgruppen im satz. Orthogonale projektion → → des vektors → auf die durch → bestimmte richtung zwei vektoren a → {\displaystyle {\vec {a}}} und b → {\displaystyle {\vec {b}}} sind genau dann orthogonal, wenn ihr skalarprodukt null ist, also Orthogonale projektion · orthogonalprojektion · senkrechte projektion.
Orthogonale Projektion Beispiel: Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren.
